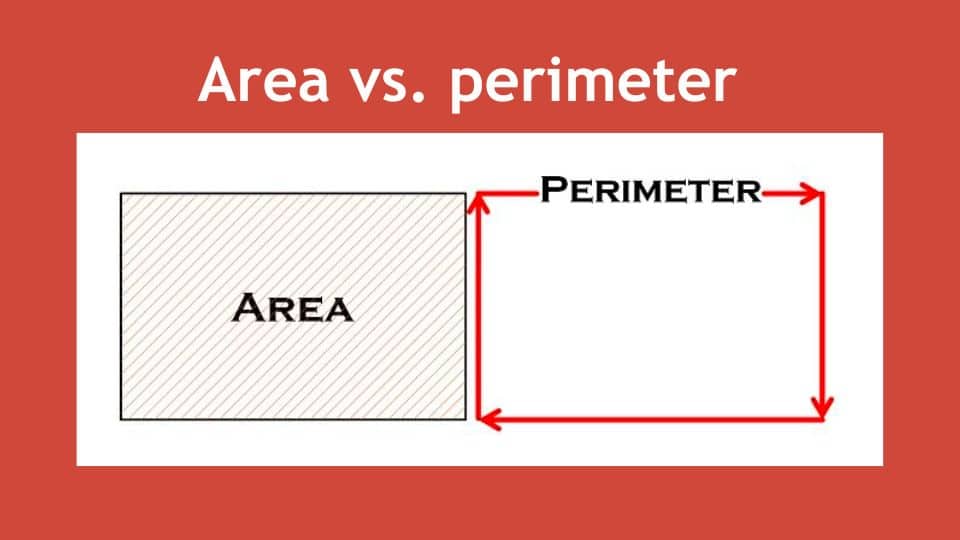
When we look at any two-dimensional shape, whether a rectangle, a circle, or a triangle, two fundamental properties often come into play: area and perimeter. These terms are essential in mathematics, particularly in geometry, and while they are related, they describe very different aspects of a shape.
Understanding the difference between area and perimeter is crucial in mathematics and various real-world applications such as construction, design, and even daily life activities.
What is perimeter?
The perimeter is the total distance around the edge of a two-dimensional shape. Think of it as the length of the boundary that encloses the shape. For instance, if you were to walk around the edge of a rectangular park, the distance you walk would be the park’s perimeter.
Formulae for perimeter:
- Rectangle: P=2×(l+w), where l is the length and w is the width.
- Square: P=4×s, where s is the length of a side.
- Triangle: P=a+b+c, where a, b, and c are the lengths of the sides.
- Circle: P=2×π×r, where r is the radius (also known as the circumference of a circle).
Understanding perimeter with an example: Imagine you have a rectangular garden that is 10 meters long and 5 meters wide. The garden’s perimeter would be: P=2×(10 m+5 m)=2×15 m=30 m. This means you would walk 30 meters if you traced the garden’s boundary.
What is area?
The area, on the other hand, refers to the amount of space enclosed within a shape. It measures the surface of the shape in square units. Essentially, if you were to cover the shape with square tiles, the area would be the number of tiles required to cover it completely.
Formulae for area:
- Rectangle: A=l×w (length × width)
- Square: A=s×s (side × side)
- Triangle: A=1⁄2×b×h (1⁄2 × base × height)
- Circle: A=π×r2 (3.14 × (ratio × ratio))
Understanding area with an example: Using the same rectangular garden that is 10 meters long and 5 meters wide, the area would be: A=10 m×5 m=50. This indicates that the garden covers 50 square meters of surface.
Key differences between area and perimeter
- Definition:
- Perimeter: Measures the length around the boundary of a shape.
- Area: Measures the surface enclosed within the boundary of a shape.
- Units:
- Perimeter: Measured in linear units such as meters, feet, or inches.
- Area: Measured in square units such as square meters, square feet, or square inches.
- Dimensionality:
- Perimeter: One-dimensional, as it only involves the length.
- Area: Two-dimensional, as it involves both the length and width (or equivalents like base and height).
- Calculation focus:
- Perimeter: Focuses on the sum of the lengths of all sides.
- Area: Focuses on multiplying lengths to find the extent of the surface.
Real-world applications
Understanding the difference between area and perimeter is important in various fields:
- Architecture and construction: When designing a building or laying out a garden, perimeter measurements are used to determine the length of fencing required or the amount of baseboard needed, while area calculations help in determining the amount of paint, flooring, or sod required.
- Agriculture: Farmers use perimeters to plan fencing around fields and areas to calculate the space available for planting crops.
- Interior design: In designing rooms or placing furniture, the perimeter can help understand wall lengths for decor, while the area is essential for deciding the size of carpets, tiling, or the amount of material needed to cover a space.
Misconceptions and common errors
A common misconception is confusing perimeter and area when asked to solve problems. For instance, students might calculate the perimeter when asked for the area or vice versa. To avoid this, it’s crucial to recognize whether the problem is asking for the distance around a shape (perimeter) or the space within it (area).
Conclusion
The concepts of area and perimeter are foundational in mathematics and have significant practical implications. While the perimeter relates to the boundary of a shape, the area refers to the space contained within that boundary. Understanding these differences helps solve a wide range of mathematical problems and is essential for various practical applications, from building structures to planning layouts.
Worksheets with answers
- Perimeter & shapes worksheet
- Perimeter & quadrilaterals* worksheet
- Area & shapes worksheet
- Area & quadrilaterals* worksheet
*A flat shape with four straight sides.
Edublox offers cognitive training and live online tutoring to students with dyslexia, dysgraphia, dyscalculia, and other learning disabilities. Our students are in the United States, Canada, Australia, and elsewhere. Book a free consultation to discuss your child’s learning needs.
Authored by Shanice Jordaan. Shanice holds a bachelor’s degree in education and has extensive teaching experience, having taught math for five years and English for three. She leverages her skills as an English teacher, online ESL teacher, and math and reading tutor to design engaging lessons, foster positive learning environments, and cater to diverse learning needs. Worksheets created by Caitlin Jacobs.
