
Mathematics has shaped every facet of human existence, from commerce to art, astronomy to architecture, and has been essential to human development. Its history spans centuries and continents and is a rich tapestry of inventions and discoveries. This article explores the history of mathematics, focusing on significant turning points and individuals who have influenced this vital discipline.
.
Table of contents:
- Early beginnings
- Ancient civilizations and their contributions
- Eastern contributions
- Islamic Golden Age
- Renaissance and the birth of modern mathematics
- 18th & 19th centuries: Expansion and formalization
- 20th century and beyond: Innovation and integration
- Conclusion
1. Early beginnings
Mathematics’ history starts in the Palaeolithic period. Ancient artifacts like the 20,000 BC Ishango bone from central Africa provide evidence that early humans employed crude counting techniques. Early counting techniques and possibly even a grasp of prime numbers is suggested by this artifact.
2. Ancient civilizations and their contributions
Mesopotamia
Around 3000 BC, the Sumerians in Mesopotamia—the birthplace of civilization—developed an advanced number system. The fact that they employed a base-60 system still affects how we measure angles and time. The Sumerians were succeeded by the Babylonians, who produced notable developments in geometry and algebra. They made clay tablets that contained records of their mathematical prowess, such as Pythagorean triples and solutions to quadratic equations.
Egypt
Math was very important in ancient Egypt, which is renowned for its colossal architecture. Egyptians used simple fractions and devised a decimal system. Their mastery of mathematics is demonstrated by the building of the pyramids, which had to be precisely calculated in order to attain their striking symmetry and alignment with celestial bodies. The Rhind Mathematical Papyrus, which dates to approximately 1650 BC, presents their solutions to mathematical puzzles involving concepts like area, volume, and proportions.
Greece
Greek mathematics laid the foundation for modern mathematical thought. Pythagoras, a preeminent figure, established a school that explored number theory and geometry. His famous theorem, relating the sides of a right triangle, remains fundamental in geometry. Euclid, another towering figure, compiled “The Elements,” a comprehensive collection of mathematical knowledge that served as the leading textbook for centuries. Archimedes, renowned for his work in geometry and calculus, calculated pi with remarkable accuracy and devised ingenious methods to find areas and volumes of shapes.
3. Eastern contributions
India
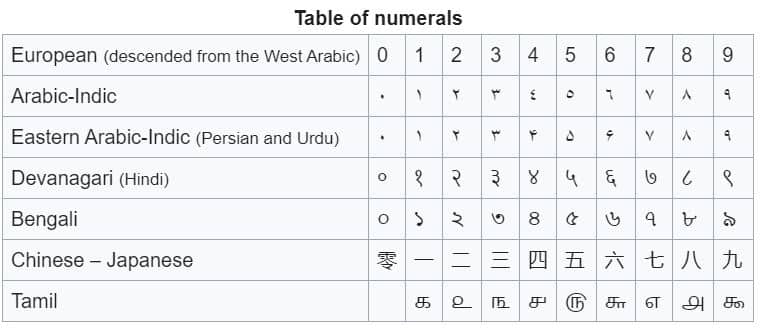
Indian mathematicians achieved notable progress, particularly in the fields of algebra and number theory. Computation and mathematics underwent a transformation with the introduction of zero in the fifth century AD. The Indian mathematician Aryabhata played a key role in the development of algebra and was the first to introduce trigonometry. In the seventh century, Brahmagupta laid down the foundation for arithmetic operations with zero and negative numbers, paving the way for future advancements in algebra.
China
In China, mathematics developed independently, with unique contributions to arithmetic and algebra. The Chinese used a decimal system and developed techniques for solving linear equations. The “Nine Chapters on the Mathematical Art,” compiled around the 1st century AD, is a comprehensive text that covers various mathematical topics, including fractions, proportions, and geometry. The Chinese also made advances in algebra, as evidenced by the work of mathematicians like Liu Hui and Zu Chongzhi, who calculated pi to seven decimal places.
4. Islamic Golden Age
During the Islamic Golden Age, spanning from the 8th to the 14th century, scholars in the Islamic world made significant contributions to mathematics. Al-Khwarizmi, often called the “father of algebra,” wrote “The Compendious Book on Calculation by Completion and Balancing,” which introduced systematic solutions to linear and quadratic equations. His work laid the foundation for algebra, a term derived from the Arabic word “al-jabr.”
Islamic mathematicians also excelled in geometry and trigonometry. Omar Khayyam, known for his work on the classification and solution of cubic equations, made significant contributions to the understanding of geometric problems. The development of spherical trigonometry by Islamic scholars like Al-Battani and Nasir al-Din al-Tusi played a crucial role in advancing astronomy and navigation.
5. Renaissance and the birth of modern mathematics
Mathematical progress reached new heights during the Renaissance, a time of rekindled interest in classical knowledge. Ancient Greek and Islamic mathematicians’ writings were rediscovered and expanded upon by European mathematicians.

.
Italy
In the 16th century, Italian mathematicians made remarkable strides in algebra and geometry. Niccolò Tartaglia and Gerolamo Cardano solved cubic and quartic equations, paving the way for future developments in algebra. Cardano’s book “Ars Magna” (The Great Art) became a seminal work in algebra.
Galileo Galilei, a pivotal figure in the Scientific Revolution, investigated motion and mechanics by using mathematical concepts. His contributions established the groundwork for classical mechanics, and his incorporation of mathematical analysis into scientific investigations signaled a paradigm shift in the use of mathematics in studying nature.
.
France and Germany
In the 17th century, French mathematician René Descartes introduced the Cartesian coordinate system, linking algebra and geometry in a new and powerful way. His work “La Géométrie” revolutionized the study of geometry and laid the groundwork for analytic geometry.
Around the same time, German mathematician Johannes Kepler used mathematics to describe the laws of planetary motion, while Isaac Newton and Gottfried Wilhelm Leibniz independently developed calculus. Newton’s “Principia Mathematica” provided a comprehensive mathematical framework for understanding the physical world, while Leibniz’s notation for calculus remains in use today.
6. 18th & 19th centuries: Expansion and formalization
Mathematical theories were expanded and formalized in the 18th and 19th centuries. Swiss mathematician Leonhard Euler made significant advances in the study of mathematical functions, number theory, and graph theory. His extensive body of work has influenced several contemporary mathematical ideas.
In the 19th century, Carl Friedrich Gauss, often called the “prince of mathematicians,” made significant contributions to number theory, algebra, and statistics. His work in complex numbers, non-Euclidean geometry, and the theory of functions greatly influenced the development of modern mathematics.
The notion of a Fourier series was first presented by the French mathematician Joseph Fourier, and it quickly gained popularity as a valuable tool for solving differential equations and analyzing periodic functions. The foundation for contemporary mathematical analysis was laid by Augustin-Louis Cauchy and Bernhard Riemann, who further formalized calculus and analysis.
7. 20th century and beyond: Innovation and integration
Mathematical progress and diversity reached previously unheard-of levels in the 20th century. As computer science grew, the application of mathematics was altered, while the advancement of topology and abstract algebra opened up new possibilities.

Set theory and logic
Set theory was developed by German mathematician Georg Cantor, who gave mathematics a strict foundation. His studies of sets’ structure and the notion of infinity had a significant impact on mathematical logic and philosophy.
The British mathematician and logician Alan Turing developed the Turing machine concept. This work laid the theoretical foundation for contemporary computers. He transformed mathematics and technology with his work on computation and algorithms. Turing is frequently referred to as the father of computer science.
Quantum mechanics and relativity
New mathematical techniques and methods were needed with the development of quantum mechanics and the theory of relativity in the early 20th century. While the theory of relativity mainly relied on the mathematical structures of differential geometry and tensor calculus, mathematicians such as Hermann Weyl and John von Neumann helped to develop the mathematical frameworks for quantum mechanics.
The digital age
The development of digital technology and computers in the second half of the 20th century changed mathematics. The advancement of algorithms, numerical techniques, and computer simulations made new paths to solving challenging issues possible. Advanced mathematical ideas like number theory and algebraic geometry are necessary for cryptography, which is crucial for secure communication in the digital age.
8. Conclusion
Human curiosity, inventiveness, and tenacity are demonstrated throughout the history of mathematics. Through the contributions of innumerable people and cultures, mathematics has developed from prehistoric counting systems to contemporary computational techniques. Its uses are still growing, spurring innovation in engineering, science, and other fields.
Pursuing mathematical discovery holds the potential to yield novel perspectives and opportunities, potentially influencing the course of human history in unanticipated ways.
Edublox offers cognitive training and live online tutoring to students with dyslexia, dysgraphia, dyscalculia, and other learning disabilities. Our students are in the United States, Canada, Australia, and elsewhere. Book a free consultation to discuss your child’s learning needs.
Sources:
Merzbach, U. C., & Boyer, C. B. (2011). A history of mathematics (3rd ed.). Hoboken, NJ: Wiley & Sons, Inc.
Pickover, C. A. (2009). The math book: From Pythagoras to the 57th dimension, 250 milestones in the history of mathematics. New York: Sterling Publishing Company, Inc.
Stedall, J. A. (2012). The history of mathematics: A very short introduction. Oxford: Oxford University Press.
Struik, D. J. (2012). Concise history of mathematics (4th ed.). New York: Dover Publications, Inc.


